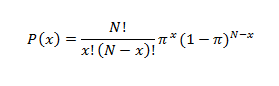Global Research

A recent series of contributions to Global Research by this author (e.g., here) contends that the U.S. government is lying about certain core aspects of the current Ebola outbreak.  One core aspect consists in the idea that the current, never-before encountered strain of Ebola we are now dealing with is more likely to be aerosolized than has been acknowledged by the U.S. government.  Another core aspect consists in the proposition that the current outbreak is attributable to U.S. sponsored bioterror. 

Now, additional Ebola information has come to light—or, at least, Ebola information that we are given to believe is true has come to light.  This article discusses why careful analysis of certain  new information suggests that while we should continue to maintain the view that the Ebola phenomenon is U.S. sponsored bioterror, we should now view the “aerosolized” issue against a background of potential fraud.  If what we have been told is true about recent, alleged U.S. Ebola cases is in fact very unlikely to be true, we are justified in suspecting that fraud is in play.

While we cannot be sure, there are now compelling, and formal, probabilistic reasons to believe that at least certain features of the U.S. Government/MSM Axis Ebola narrative are fraudulent.  Two such features are discussed herein.

The first feature concerns the apparent fact that Dr, Kent Brantly shares the same blood type, for purposes of plasma transfusion, with three U.S. citizens purportedly stricken with Ebola who are tightly connected with U.S. soil: Dr. Nick Sacra, NBC cameraman Ashoka Mukpo, and nurse Nina Pham.  Dr. Angela Hewitt remarked upon the Brantly’s second successive match, which was with Mukpo: “it’s not a likely scenario that he would again have the same blood type,” said Hewlett. “We are incredibly grateful that Dr. Brantly would take the time to do this, not once, but twice.” To the two matches mentioned by Hewitt we must now add, as mentioned just now,  the Pham match.

On this first feature, we are going to do something that innumerate, propagandist Axis MSM mouthpieces unwilling and in most cases unable to do, which is compute the probability that Brantly’s blood type matched, for plasma transfusion purposes, the blood type of Sacra, Mukpo, and Pham.  That probability, it turns out, is very low indeed.

The second suspect feature of the MSM Ebola narrative surrounds the Pham Ebola case in particular. While it may sound bombastic, the brute fact is that right now—again on formal probabilistic grounds but this time together with contextual evidence—there is very little reason to believe that Pham in fact contracted Ebola.  As you will see, this is very easily demonstrated.

Let us first address the probability of the three Brantly matches.  First, view the plasma compatibility chart here.  While for some reason we are not told what Brantly’s blood type, for plasma transfusion purposes, is, we are told that Brantly did not match Thomas Eric Duncan.  As the chart indicates, that rules out blood type AB for Brantly, since the AB type can donate to any blood type.  And, if Brantly were O, he would have matched Duncan if Duncan were an O—but in that event, all four cases would have been a match, since O donors  match with O patient groups and Brantly is said to have matched the other three cases (O donors only match with O recipients).  Since all four cases were not a match,  Brantly is not an O, and since Brantly could not have been AB, Brantly’s blood type for plasma transfusion purposes is, in view of the foregoing, necessarily either A or B.

We can now use, together with data regarding the ethnic distribution of blood types, the binomial distribution together with the product rule to derive the probability that Brantly matched the three latest, purportedly Ebola infected U.S. persons tightly connected with U.S. soil.  The binomial distribution formula is: 

Where: P(x) is the probability of x matches (in this instance x=2, referring to the two U.S. White matches, which share the same probability); N is the number of trials (here, two, since there were two U.S. White cases); and π=the probability of a U.S. White match, which, as the above-linked ethnic distribution of blood types table shows, is equal to .4 if the two U.S. White blood type matches to Brantly are A, and .11 if the two U.S. White blood type matches to Brantly are B (we are going to do the process twice, once for the A blood type and once for the B blood type.)

To get the final 3 match result with respect to the A blood type, we will use the product rule and multiply the 2 case U.S. White result by the relevant Vietnamese heritage (Pham) type A probability, which is .22.  In the case of the B blood type, we will multiply the 2 case U.S. White result by .3, which is the relevant Vietnamese heritage type B probability.  We use the product rule to account for Pham’s case because her probability of a match is different than the two U.S. White cases; nevertheless, the probability of her matching blood type is presumably independent, just as the probabilities of matches for the other cases are—so we can use the product rule to finalize the probability of the three matches (we should add that if the probabilities of the three matches to Brantly are not independent, some form of fraud is almost certainly afoot).

If Brantly’s blood type is A, application of the above procedure yields a probability (keeping in mind that 0!=1) that Brantly matched the three cases of: .16 * .22, which equals .0352—a very low probability indeed.  If Brantly’s blood type is B, the procedure yields a probability of three matches of .0121* .3, which gives .00363—a very, very low probability indeed.

So, in sum, in the best case scenario (the Brantly Type A case) for the U.S. Government/MSM Axis, there is, on current information, a 96.48% chance that the Axis is lying when it says Brantly matched the three cases. If, under the narrative, Brantly is type B, there is, on current information, a 99.64%  chance that the Axis is lying about the three matches (we could combine these two probabilities by weighting, but with probabilities so low in either case, what, in the words of Fascist Hillary Clinton, difference does it make?)

Now to the specific Pham scenario. The CDC asserts that Pham has been infected, and that she was infected due to a breach of protocol.  Formal probabilistic considerations together with contextual evidence, however, suggest that there is very little reason, at present, to believe that Pham has in fact been infected.  By its own admission, the CDC cannot say what that breach of protocol was.  Here we must add that, just after the evidently miraculous blood transfusion by the bearded, Christ-like Brantly, Pham’s condition has now been upgraded to “good.”   We might also add that as of this writing none of Duncan’s Dallas contacts in the apartment seem to have been infected, and what’s become of them anyway?  They seem to have vanished, and the Axis MSM is, of course, uninterested.

But these contextual observations are hardly the only reason to question whether Pham in fact contracted Ebola.  In fact, formal probabilistic reasons pertaining to Bayes’ theorem counsel pronounced skepticism.

From a formal standpoint, the only evidence we have been given that Pham is in fact infected with Ebola is that a positive test result was returned.  Without more, however, the positive test result is meaningless.  To see this, consider that there is a very easy way to design a test that captures all cases that are really positive: just have the test report a positive result in every instance, whether the subject is in fact positive or negative.  The more important point, though, is that even if the probability that Pham would test positive if she was not positive (that is, the false positive probability) is very low, without information about the prior probability that Pham was even in a position to, with a meaningful probability, contract the disease, the test result can be extremely misleading—so much so that it can be far more likely to be wrong than right.

This sounds very counterintuitive to many people, and so a brief explanation is in order.  Suppose that in a population of 10,000 people only 10 have Ebola.  If only 1% of cases produce a false positive under this supposition, 100 cases will test positive that do not in fact have the disease.  So, even if the Ebola test used on Pham correctly identifies 100% of the true positive cases, the 10 positive cases correctly identified would be overwhelmed by the 100 false positives, such that a positive test result would yield only a 10/100, or 10% chance of Ebola infection.  In short, a great deal depends on just what the relevant “prior” population and associated probability is.

This is precisely why the limited information on just how Pham is supposed to have been infected is so disconcerting; it goes to how small or large the prior probability is, and hence to the number of potential false positives in cases like hers.  And, obviously, if Pham had no exposure whatsoever to Duncan, the positive test result would mean precisely: zilch, or right next to it.

True, via the New York Times, we have this from a “college friend” of Pham’s:

“Ms. Mitchell, Ms. Pham’s college friend, said the two spoke only fleetingly about her work at what has become the center of Ebola in the United States. Mr. Duncan was treated on Ms. Pham’s unit, Ms. Mitchell said in a brief telephone interview on Sunday, but Ms. Pham had said that only “at one point in time did she have him.””

So, at one point in time Pham is asserted, by way of hearsay evidence, to have had contact with Duncan?  It has been asserted that Pham had contact with Duncan “from the day he was admitted to the hospital”, but why should we believe this, especially since many MSM people (e.g., the Daily Mail) assert Brantly had miracle matches that are cast into grave doubt by the preceding analyses?  And, if what these folks say about Pham’s repeated Duncan contacts is correct, why doesn’t Mitchell echo them?  And, so far, no attendees of Duncan other than Pham have been reported as infected; we shall of course see what the future brings in this regard.

Also in connection with the prior probability issue, interested readers may want to examine an academic article entitled “Incubation Period of Ebola Hemorrhagic Virus Subtype Zaire.” There, we find evidence that even strong contacts with the Ebola-infected can leave substantial probabilities that infection will be avoided—even over time periods as long as a week.  True, that might help explain why Dallas apartment Duncan contacts have not contracted Ebola, and yet, with at least 70 health care workers supposedly exposed and no additional Ebola diagnoses as of now, plentiful questions remain.

In view of all of the above, is it beyond all reason to suppose that Pham, and conceivably even Brantly, have been duped—along with much of the rest of the “bioterrorized” world—at least with respect to purported U.S. citizen, U.S. soil Ebola cases?

Dr. Jason Kissner is Associate Professor of Criminology at California State University. Dr. Kissner’s research on gangs and self-control has appeared in academic journals. His current empirical research interests include active shootings. You can reach him at crimprof2010[at]hotmail.com